Qual o segredo da matemática?
Muito além da contagem, uma linguagem que pode expressar ideias verificáveis
Muita gente se pergunta - com certo descontentamento - o que a matemática tem que a torna tão especial a ponto de ser considerada a base da ciência, da inovação e do desenvolvimento econômico. Por que contar as coisas é mais científico do que observar e descrever em palavras o que se percebe na realidade?
Hoje em dia, há um debate sobre o papel da matemática na educação, muito em virtude das baixas dos estudantes brasileiros em testes comparativos internacionais1, além dos resultados do próprio INEP2, que mostram que boa parte dos jovens não tem o conhecimento mínimo para a etapa de ensino na qual está matriculada3. Há uma mobilização de vários setores no país em prol do fortalecimento do ensino de matemática, o que é muito importante e, sem dúvida alguma, deve ser implementado com urgência.
Mas muita gente ainda se pergunta: por que aprender matemática é importante? Com certeza, a matemática, por si só, não é a única fonte do conhecimento e, mais ainda, da qualificação necessária para a compreensão e promoção do avanço nas condições econômicas e sociais do país. Todas as áreas de ensino, com suas competências e habilidades, devem ser reforçadas no Brasil. O problema dos baixos índices de aprendizagem é um problema do sistema de ensino como um todo. Não se pode fortalecer uma área e negligenciar as demais.
Ainda assim, há pessoas que, direta ou indiretamente, defendem uma ideia de que somente o conhecimento de matemática é necessário para se criar inovações e desenvolvimento. Os demais conteúdos são acessórios. Não são. Se um estudante passasse todo o seu tempo escolar apenas aprendendo matemática (talvez apenas junto com a língua portuguesa, como desejam alguns), suponhamos que com os melhores métodos, a melhor infraestrutura escolar e os melhores docentes, ainda assim teríamos uma nação limitada em sua capacidade de compreender a complexidade dos problemas reais da vida, de buscar soluções inovadoras para esses mesmos problemas e de enfrentar os desafios estratégicos que o desenvolvimento econômico e social exigem para o presente e para o futuro.
Ao contrário do que pregam certos coachs em política educacional (com experiência incerta em sala de aula), aumentar o tempo de ensino de matemática em detrimento dos demais conteúdos não é a solução nem para os problemas do ensino da matemática, nem para o problema do ensino no país.
Por outro lado, negar a matemática como parte essencial de uma formação intelectual criativa constitui um equívoco sério. É tão errado ver a matemática como o conteúdo que, isoladamente, vai elevar o nível de inteligência e desenvolvimento do país, quanto ignorar que a matemática tem um papel fundamental para permitir o avanço do conhecimento em qualquer área do conhecimento, incluindo as ciências humanas.
Conforme discutimos no texto “A matemática faz sentido para as humanidades?”4, a dicotomia entre matemática e ciências humanas representa um obstáculo prejudicial ao atribuir às humanidades um ethos que não só se distancia, mas se opõe por princípio ao conhecimento matemático. Essa dicotomia sugere, de forma explícita, que os indivíduos nascem predestinados a um de dois caminhos: ou ao domínio da explicação objetiva da realidade pelos números — considerados frios, precisos e regidos por regras inflexíveis — ou ao território da compreensão empática, da aproximação da realidade pela sensibilidade e do pensamento crítico. Uma dualidade irreal, construída para justificar guetos acadêmicos. Essa visão tolhe o desenvolvimento pleno da capacidade humana, supondo que tais dimensões, explicação e compreensão sejam mutuamente excludentes.
A formação matemática deve ser integrada aos conteúdos criativos de todas as disciplinas, desde o ensino fundamental, incluindo as áreas de humanas5. A matemática é uma linguagem fundamental para representar ideias que podem ser analisadas, testadas e fundamentadas em dados. O verdadeiro desafio, portanto, não está em optar entre a matemática e as demais áreas do saber, mas em articulá-las de maneira coerente, promovendo uma formação que valorize simultaneamente o raciocínio lógico, a competência linguística, a análise histórica e social, e a sensibilidade estética e ética.
Um caminho para além dos argumentos de autoridade
Voltamos, então, à questão inicial: por que a matemática é tão importante para o pensamento criativo? Não é pelo exercício de memorização dos cálculos, nem pelas fórmulas em si. Não é pela “exatidão” ou “rigor”, muito menos pela “imparcialidade”.
Para refletir sobre a articulação entre os recursos matemáticos e as demais áreas do conhecimento (especialmente sob a perspectiva das ciências humanas) é fundamental ter o entendimento de que a matemática não é um bloco monolítico de saber, mas sim uma área vasta, diversa e historicamente construída ao longo de milênios. Assim como ocorre em todos os campos do conhecimento, também na matemática coexistem consensos e dissensos, linhas de pesquisa distintas, subcampos e especializações que, frequentemente, se organizam em torno de diferentes correntes de pensamento. O debate na estatística entre frequentistas e bayesianos é um exemplo.
Longe de ser um território unificado, ao longo da história, a matemática abrigou disputas epistemológicas, divergências conceituais e diferentes formas de abordagem, o que a aproxima, mais do que se imagina, como conhecimento em construção, da complexidade própria das ciências humanas. Mas, diferente das humanidades, nas áreas da matemática, os debates se transformaram em um conjunto de postulados logicamente comprovados, que formam um corpo sólido e coerente, que permanece comum a todos os seus subcampos e aplicações.
Nas ciências humanas prevalecem as disputas e interpretações segmentadas, onde múltiplas abordagens convivem (e muitas vezes colidem) em torno da autoridade dos proponentes de conceitos, métodos e até das finalidades do conhecimento. A incorporação de tabelas, gráficos e utilização de ferramentas computacionais não é um antídoto para essa situação das ciências humanas de fragmentação e submissão da reflexão aos argumentos de autoridade. Há um pensamento comum que espera que, onde haja matemática, não haja polêmicas, porque a matemática é exata! Sim, a matemática é exata, mas as pessoas não são, nem na área de matemática!
Quando uma ideia é expressa em termos matemáticos, não se elimina automaticamente o espaço para divergências. O primeiro segredo e importância da matemática não está em ser isenta de controvérsias, nem por isentar de polêmicas os argumentos que a utilizam como ferramenta para expressão e demonstração. A matemática é um instrumento do conhecimento, construído por pessoas, em um processo contínuo e logicamente fundamentado de revisão de erros.
O primeiro segredo da matemática não é, portanto, conferir um status de verdade inquestionável a um postulado qualquer. Isso seria um dogma e não uma expressão da ciência. O segredo é oferecer meios para a revisão crítica de uma proposição a partir de um conjunto coerente de regras lógicas, indo além6 das disputas nominais, baseadas em argumentos de autoridade, princípios éticos ou ideológicos.
A matemática possui uma coleção de ferramentas que nos permite transformar os erros do pensamento em oportunidade para se descobrir os acertos, esse é o primeiro segredo que a torna indispensável para qualquer campo do saber.
Uma linguagem que permite expressar relações inferenciais
Como é possível que a matemática possa transformar os erros do pensamento em oportunidade para se descobrir os acertos em qualquer campo do saber? Por causa da sua capacidade de representar de forma relacionada os elementos e suas propriedades.
Essa representação permite inferir relações e padrões que, à primeira vista, podem estar invisíveis. Para compreender os fenômenos sociais, é necessário organizar a complexidade que, sem as ferramentas adequadas, se apresenta como caótica e desconexa. A partir dessa representação é que se consegue identificar os fatores que explicam logicamente os fenômenos e os processos de mudança.
A linguagem matemática ajuda não só a representar e a transmitir as ideias, mas, sobretudo, é indispensável como um meio facilitador para a exposição do processo de inferência. A matemática é ensinada muitas vezes como regras prontas para solucionar problemas prontos. Mas, deveria ser vista como uma ferramenta para auxiliar o pensamento na descoberta do que ainda não se sabe, com a capacidade de comunicar a outras pessoas não só as soluções prontas, mas todo o caminho, passo a passo, de construção da explicação, o que permite a reprodutibilidade do estudo.
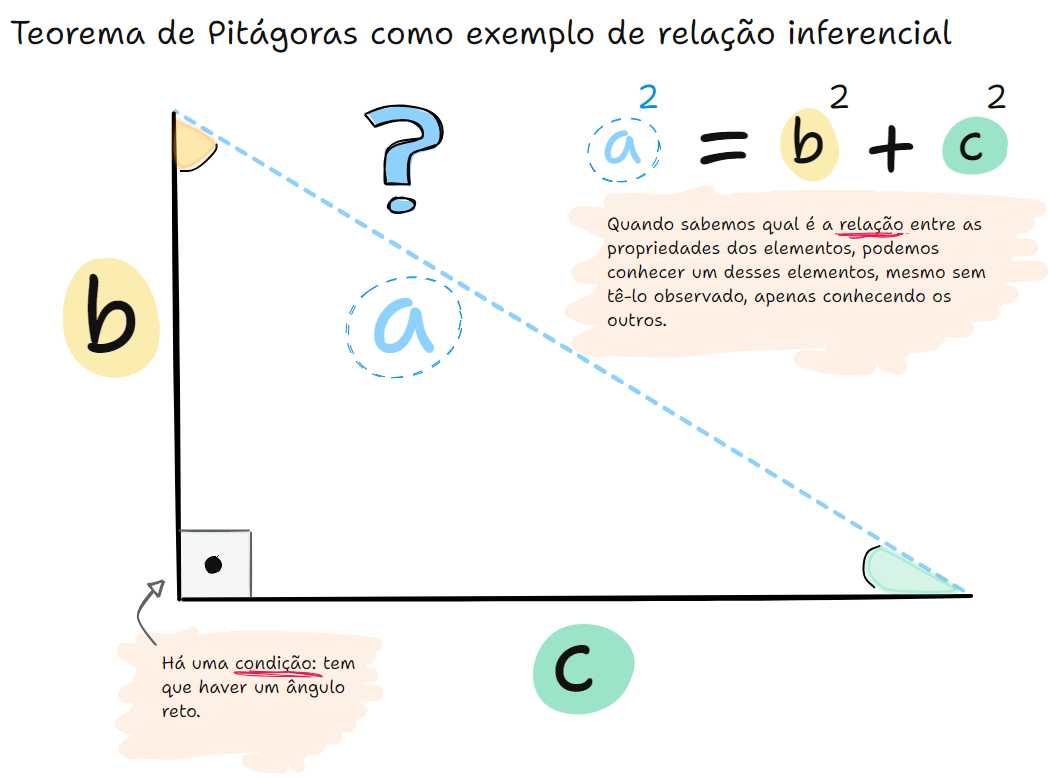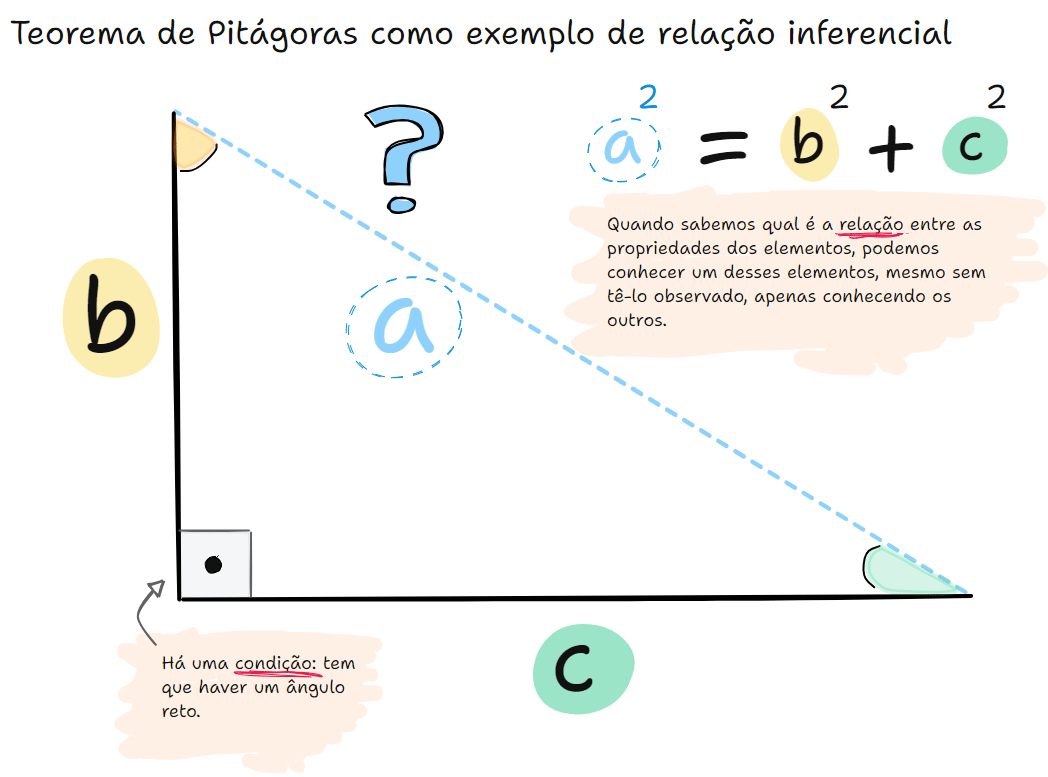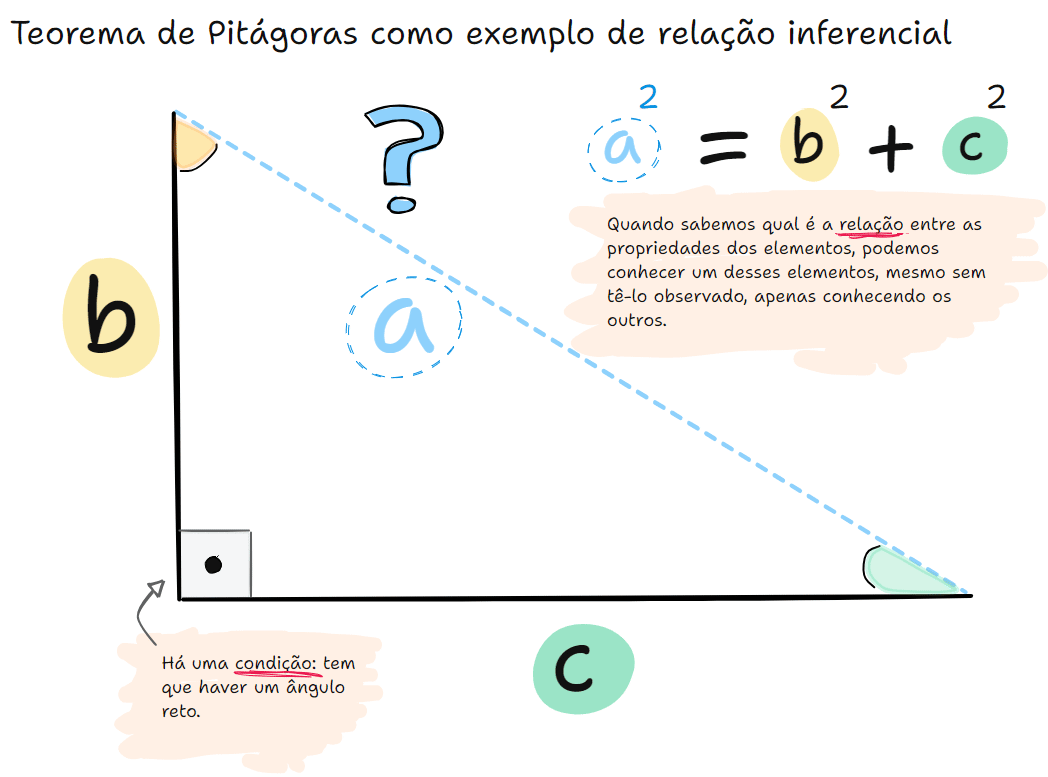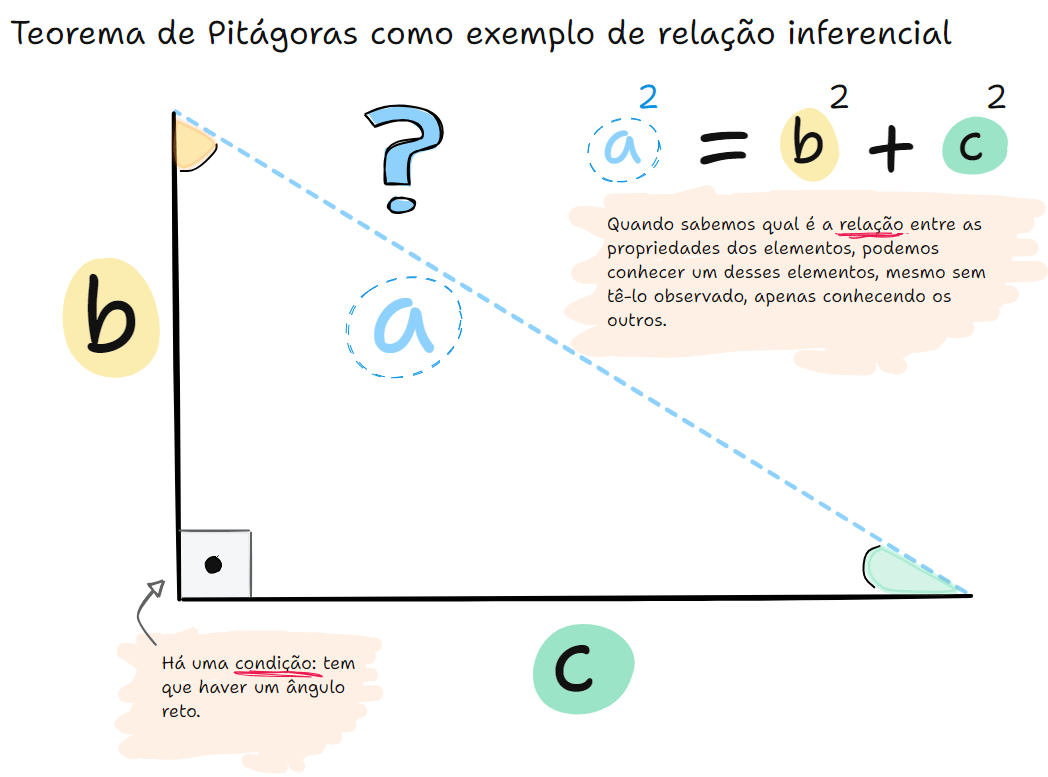
Vamos ilustrar isso com uma equação, que é a forma mais comum de visualizarmos uma relação entre termos em matemática. Vamos usar como exemplo a equação do teorema de Pitágoras.
O Teorema de Pitágoras afirma que, em todo triângulo retângulo, a soma dos quadrados dos catetos é igual ao quadrado da hipotenusa (ou seja, a² = b² + c²). Essa relação não foi definida só por observação empírica. Foi demonstrada a partir de princípios geométricos. A validade do teorema não depende da medição de um número finito de triângulos: ela é garantida logicamente para todos os triângulos retângulos possíveis, porque sua demonstração segue regras dedutivas dentro do sistema da geometria euclidiana.
Uma equação, que tanto assusta estudantes que optam pelo campo das humanidades, pode ser entendida como uma forma de representar um conjunto de regras, do mesmo modo que a gramática. Por exemplo, a norma gramatical em língua portuguesa que diz que "toda palavra oxítona terminada em a, e ou o, seguida ou não de s, deve ser acentuada" é também uma representação estruturada do pensamento. Essa regra cumpre duas funções: explicativa, ao justificar por que palavras como “você” recebem acento, e normativa, ao nos orientar sobre como acentuar palavras para uso correto da língua portuguesa e, assim, procura garantir que as pessoas se comuniquem na mesma língua. Do contrário, sem uma norma padrão, em pouco tempo, cada falante da língua estaria se expressando em seu próprio dialeto, o que dificultaria o alcance da comunicação.
Qual é, então, a diferença entre uma regra de representação gramatical e uma regra de representação matemática, como o Teorema de Pitágoras? A distinção não está na forma externa da expressão, mas na natureza do sistema de regras e nos tipos de relações que cada linguagem procura descrever. Ou seja, o que torna a linguagem matemática diferente, no caso, da linguagem gramatical não são as letras (a, b, c) nem os símbolos (=, +), tampouco o fato de cada letra representar uma quantidade. A diferença é que, enquanto a regra gramatical cumpre uma função explicativa e normativa, a regra matemática cumpre uma função explicativa e inferencial. Ela nos permite deduzir, a partir de certas condições, aquilo que logicamente se segue, gerando novas conclusões a partir de um conjunto inicial de premissas.
Tanto a regra gramatical quanto a matemática se sustentam em princípios que são definidos com rigor. Na gramática, oxítonas não são paroxítonas, nem proparoxítonas. A distinção é rigorosa, mas a regra gramatical não precisa ser provada. A regra é estabelecida como norma. Por outro lado, o rigor da matemática está na demonstração de que uma determinada relação entre propriedades será sempre válida, desde que se cumpram as condições previamente estabelecidas. A prova matemática é o processo lógico que verifica se essa relação é compatível com os princípios e regras fundamentais do sistema matemático como um todo — ou seja, se ela pode ser deduzida de forma coerente a partir das definições, axiomas e teoremas já estabelecidos.
Uma vez provada, a regra matemática passa a ter uma função inferencial: ela permite deduzir informações desconhecidas a partir de dados conhecidos. Em outras palavras, se compreendermos a relação entre as propriedades de certos elementos, poderemos conhecer o valor ou comportamento de um deles, mesmo sem tê-lo diretamente observado — basta conhecer os demais e aplicar a estrutura lógica da relação.
Esse é um dos principais segredos que torna a matemática tão importante para todas as áreas, incluindo as humanidades. Não é a exatidão por si só, o rigor ou a indiferença com relação às paixões humanas, mas a capacidade de nos permitir conhecer o desconhecido a partir do que já sabemos sobre o mundo. É o que amplia nossa capacidade de transformar o que sabemos em possibilidade de conhecermos o que ainda nos é desconhecido. E, ainda por cima, nos ajuda a rever aquilo que julgávamos saber, mas que, na verdade, estávamos errados. Muito além da contagem em si mesma, a matemática é útil por ser uma linguagem para expressar ideias verificáveis.
Certo, isso vale para a compreensão da natureza! Mas, vale também para o comportamento humano?
Uma das grandes questões sobre o uso de matemática em ciências humanas está na ideia de que a captura de padrões quantitativos só é possível para os elementos da natureza. As pessoas, dotadas de livre arbítrio e de consciência, não são passíveis de serem estudadas com números e métodos matemáticos. Isso seria uma redução metodológica ingênua, incapaz de compreender o espírito humano.
Será mesmo? O que você pensa sobre isso?
Vamos continuar conversando sobre esse tema no próximo texto…
Confira a reportagem: Brasil tem deficit em matemática entre 70% dos estudantes
Acesse na página do Instituto Nacional de Estudos e Pesquisas Educacionais Anísio Teixeira (Inep) o conjunto de Avaliações e Exames Educacionais disponíveis, como o SAEB, ENAD, ENEM entre outros.
Além de questões pedagógicas, parte do problema tem relação com as disparidades socioeconômicas, não só no Brasil, mas em vários outros países. Veja mais detalhes no estudo divulgado pelo Iede. O cenário do ensino matematica no Brasil: o que dizem os indicadores nacionais e internacionais
Você pode ler o texto na íntegra em: A matemática faz sentido para as humanidades?
Assim como as humanidades devem se abrir ao pensamento matemático, o ensino da matemática precisa incorporar as humanidades, começando pela compreensão histórica do desenvolvimento de seus conteúdos.
“Ir além” não significa ignorar as disputas ou as diferenças que fundamentam os argumentos contrários. “Ir além” significa não se deixar aprisionar por elas e pelas armadilhas teóricas decorrentes. “Ir além” significa ir além da divergência, olhar mais longe, superar os erros e dar um passo em frente, avançando o conhecimento.